| CLICK HERE FOR INDEX PAGE | |
| FORCES | |
| V. Ryan © 2002 - 2010 | |
| PDF FILE - CLICK HERE FOR PRINTABLE WORKSHEET 1 | |
| PDF FILE - CLICK HERE FOR PRINTABLE WORKSHEET 2 | |
|
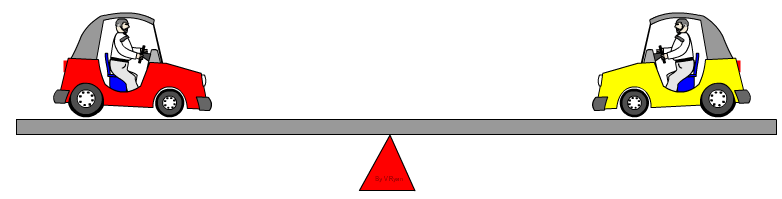
The diagram below clearly shows a state of
equilibrium. The cars on either side of the seesaw are exactly the
same in weight and height, in fact they are the same model. As a result, the
seesaw stays level. |
|
|
|
|
|
The cars are in a 'state of equilibrium' because the weight on either side is exactly the same |
|
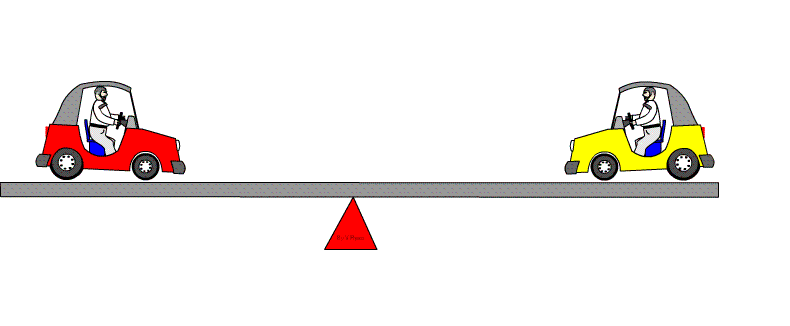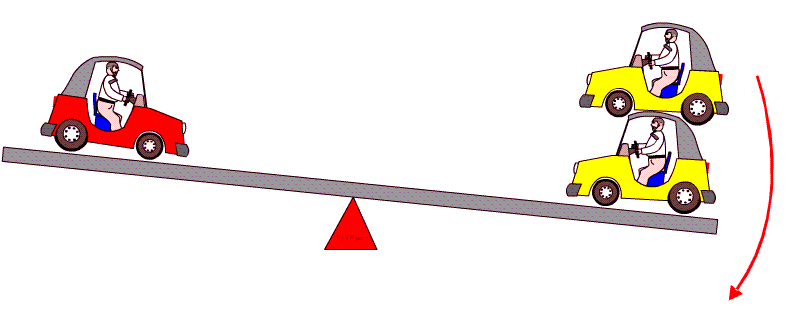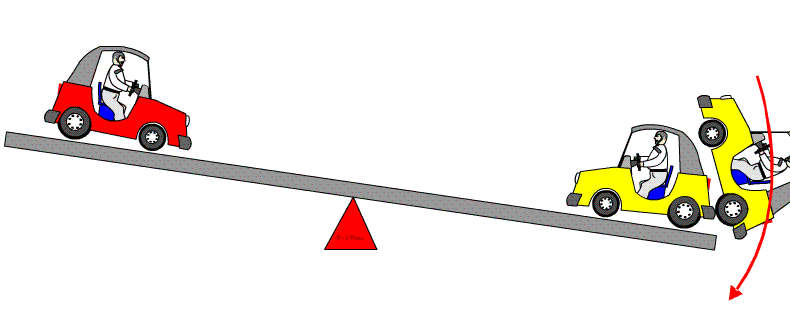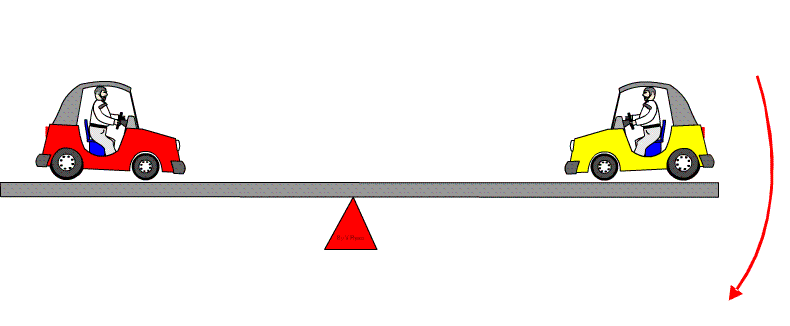
| If an extra
car is added to the right hand side (see diagram below), then the seesaw
will turn in a clockwise direction - called a clockwise moment.
Alternatively, if more cars are added to the left hand side, the seesaw will turn in an anticlockwise direction - called an anticlockwise moment. |
|
 |
|
|
|
|
| A clockwise moment as an extra car is added to the right side | |
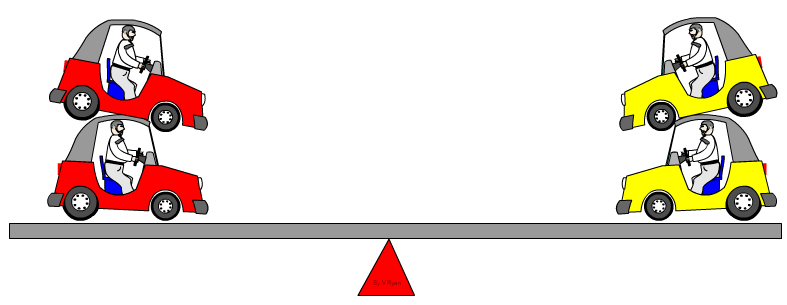
| If the seesaw is to be in equilibrium, the clockwise moments must be equal to the anticlockwise moments. The seesaw is back in ‘equilibrium’ because a second car has been added to the left hand side, as well. | |
 |
|
|
If the seesaw is to be in equilibrium then the clockwise moments must be equal to the anticlockwise moments. |
|
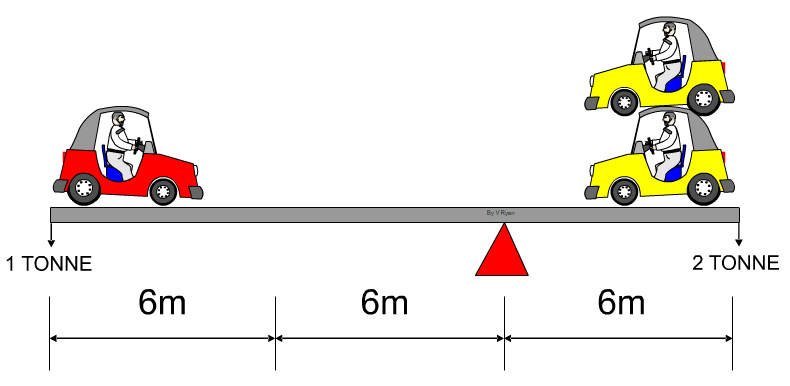
| A state of equilibrium is also seen below. Each of the cars weighs the same (1 Tonne). Despite the fact that there is only one car on the left-hand side, the moments balance because, the car on the left-hand side, is twice the distance from the fulcrum, compared to the cars on the right-hand side. (see the calculation below). | |
 |
|
| CLOCKWISE
MOMENTS = ANTI-CLOCKWISE MOMENTS 1 TONNE X 12m = 2 TONNE x 6m 12 = 12 STATE OF EQUILIBRIUM |
|
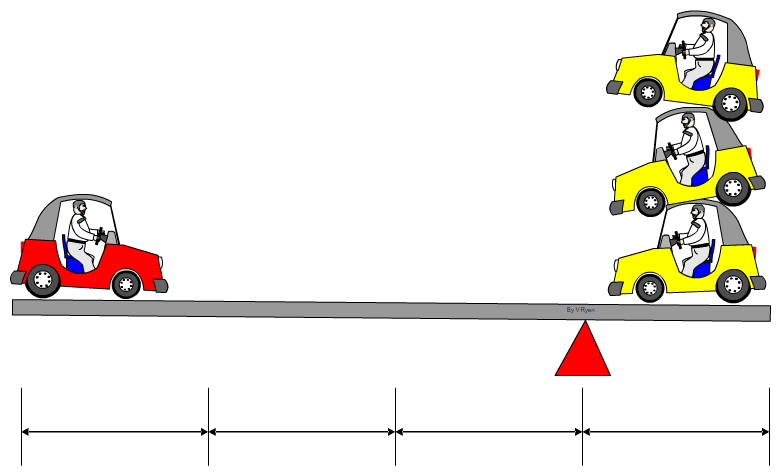
| A state of equilibrium exists below. The single car on the left, balances the three cars on the right-hand side. This is because, the single car is three times the distance from the fulcrum, compared to the three cars on the right-hand side. Both sides of the fulcrum balance. | |
 |
|
|
QUESTIONS |
|
|
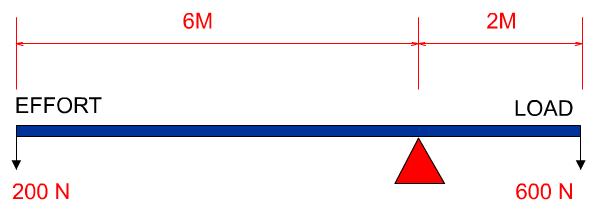
1. The diagram below shows a lever where an effort of 200 N balances a load of 600 N. The effort force is 6 metres from the fulcrum. The load force is two metres from the fulcrum. |
|
 |
|
|
Clockwise moment = 600 x 2 Nm Anti-clockwise moment = 200 x 6 Nm In a state of equilibrium, clockwise moments = anti-clockwise moments 600 X 2 Nm = 200 x 6 Nm 1200 = 1200
|
|
|
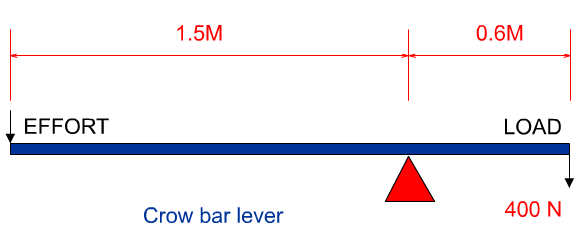
2. In the diagram below a crow-bar is used to move a 400n load. What effort is required to move the load?
|
|
 |
|
|
Clockwise moments = 400 N x 0.6 m Anticlockwise moments = effort x 1.5m In equilibrium; clockwise moments = anti-clockwise moments 400 x 0.6 = effort x 1.5 effort = 400 x 0.6 1.5
effort = 240 1.5
= 160 N
|
|
|
|
|