| CLICK HERE FOR INDEX PAGE |
| |
| STATIC AND DYNAMIC LOADS AND MECHANICAL ADVANTAGE |
| V.Ryan © 2015-2023 |
| |
 |
| |
| PDF FILE - CLICK HERE FOR PRINTABLE WORKSHEET |
| |
| CLICK HERE FOR POWERPOINT VERSION OF WORKSHEET |
| |
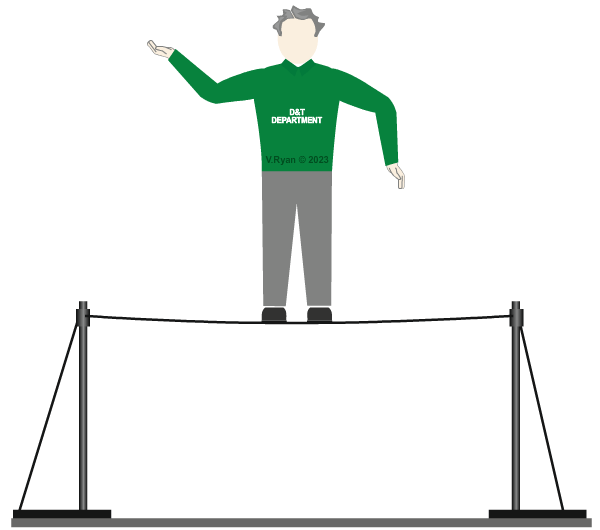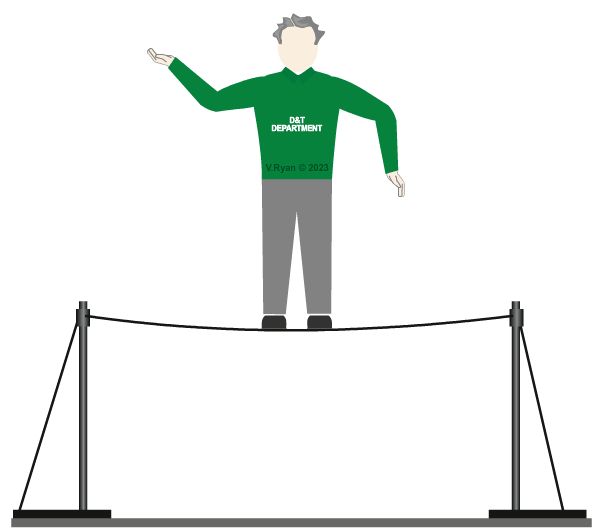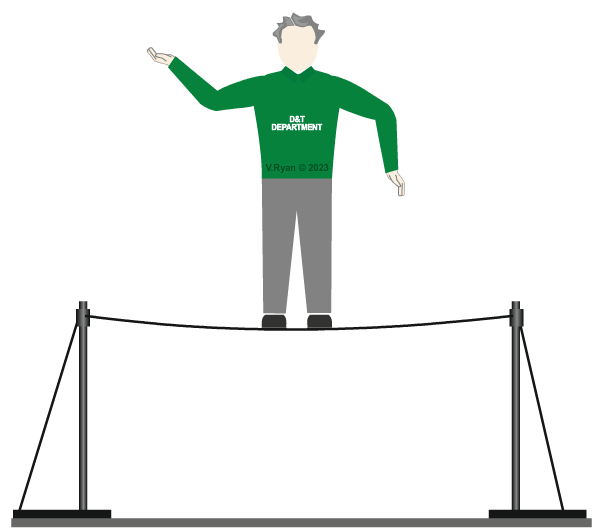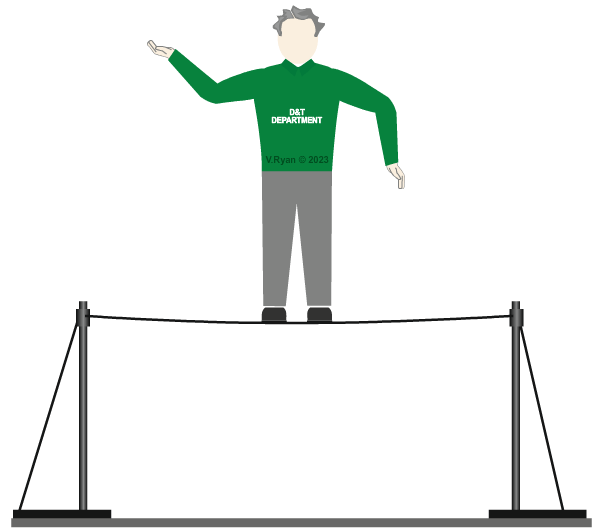
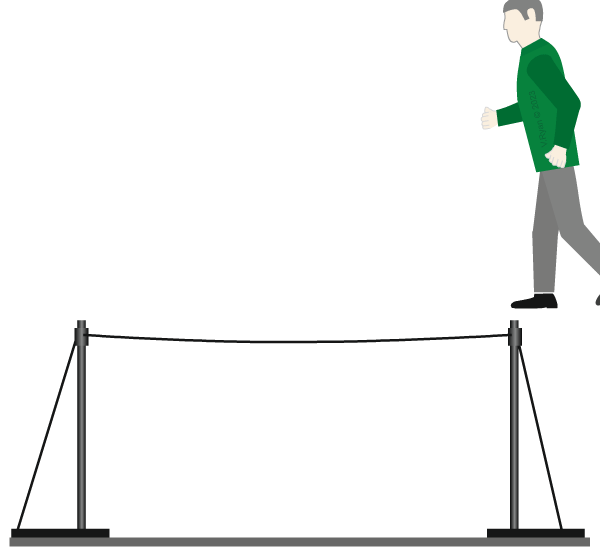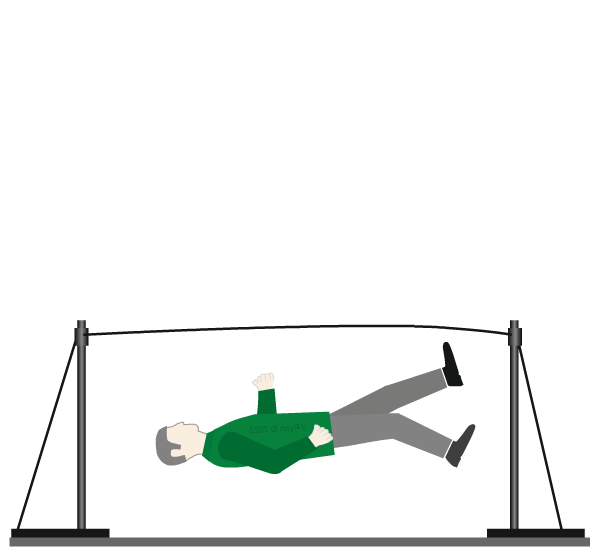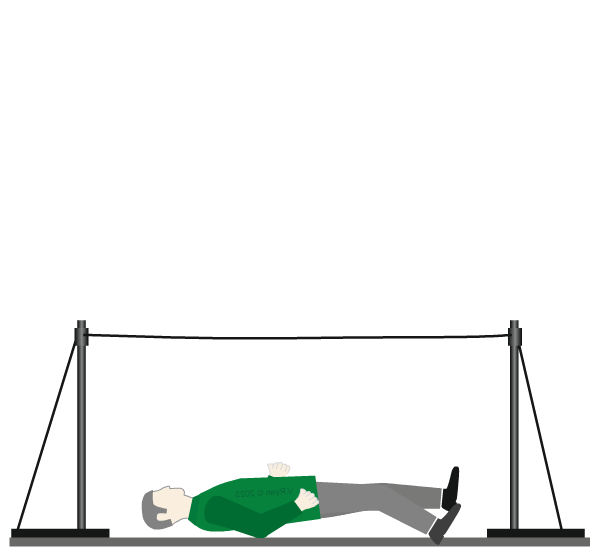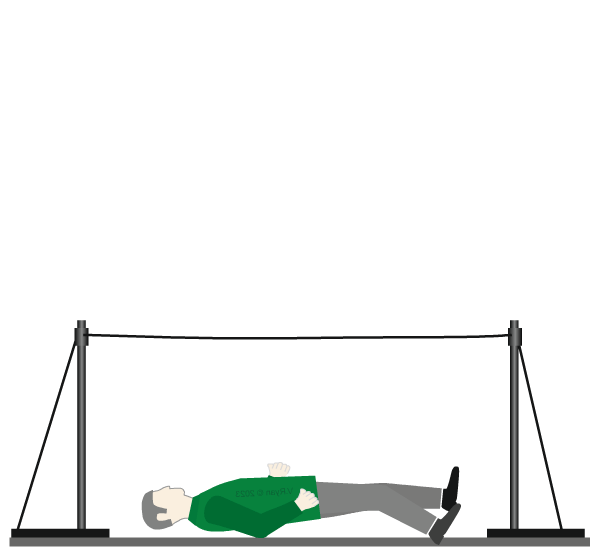
| Our tightrope walker a static load. He stands still at the centre of the tightrope. The tightrope dips with the weight applied to it, but stays in that position. |
| |
 |
| |
|
|
| |
| Our tightrope walker takes a deep breathe and starts to walk across the rope. He is now a dynamic load, as he is moving and yet still exerting a weight downwards. |
| |
 |
| |
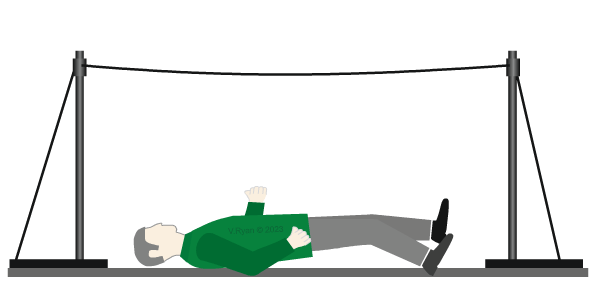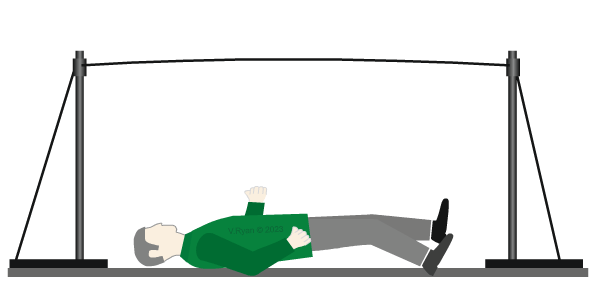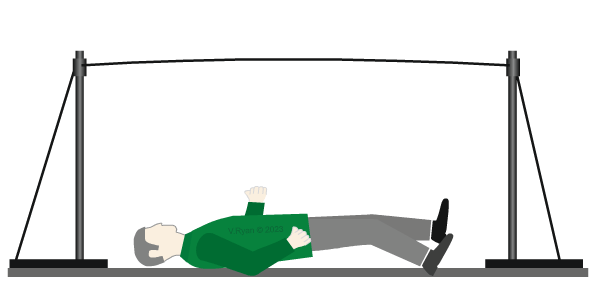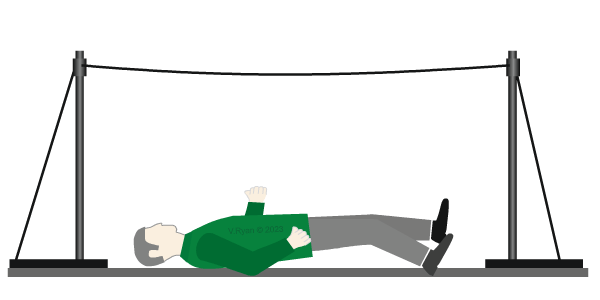
| Having fallen off the tightrope, our tightrope walker lies still on the floor. He is again a ‘static load’, as the weight of his body still exerts a force on the floor. |
| |
 |
| |
|
|
| |
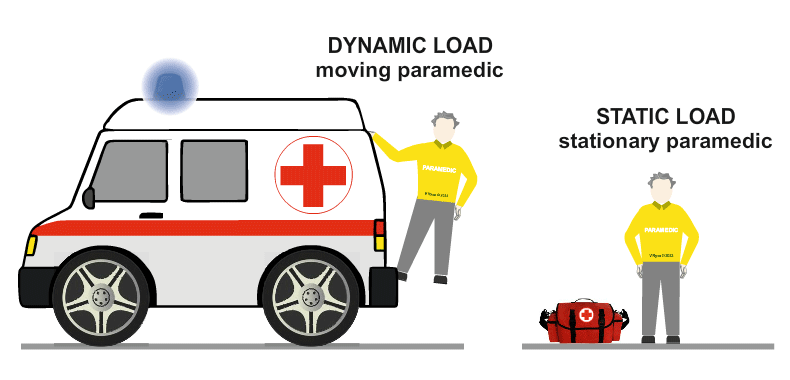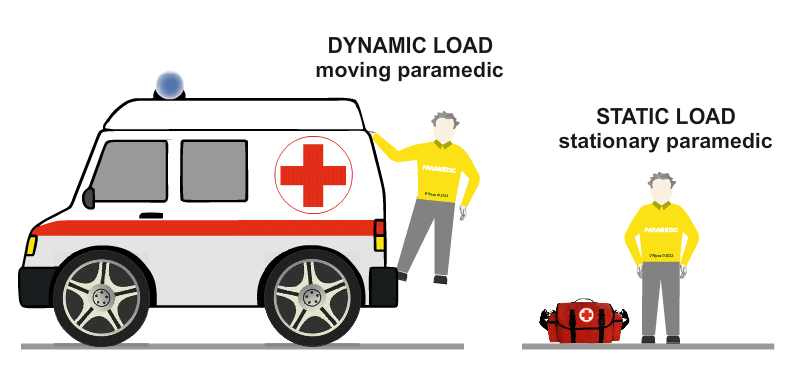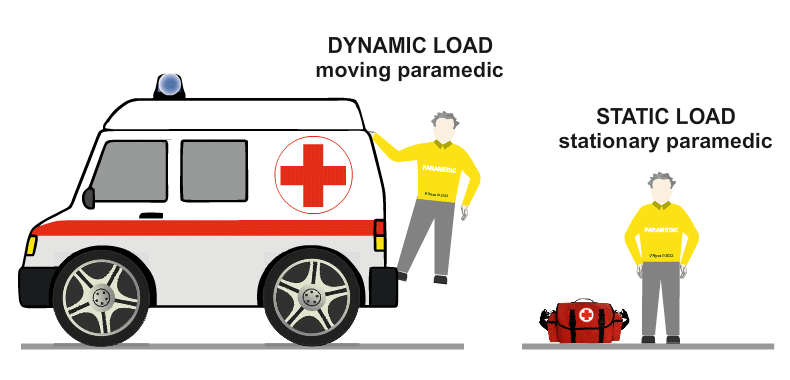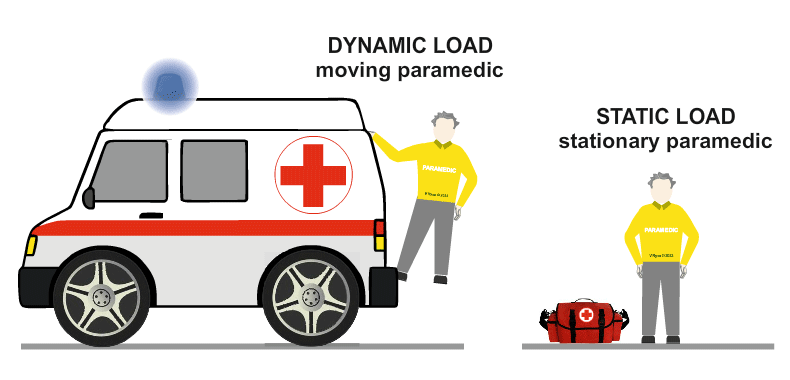
| Highly trained paramedics are called to take care of the stationary tightrope walker. |
| |
 |
| MECHANICAL ADVANTAGE |
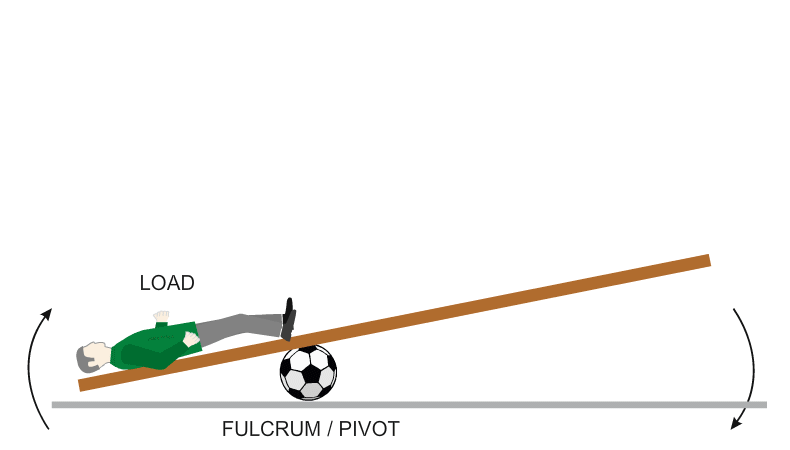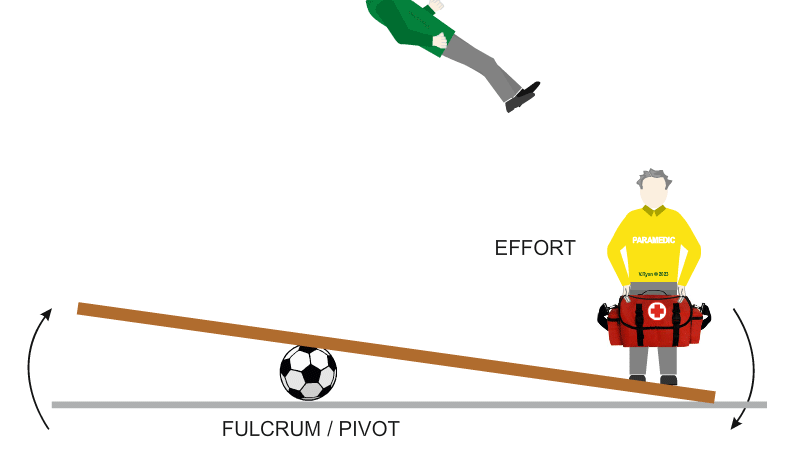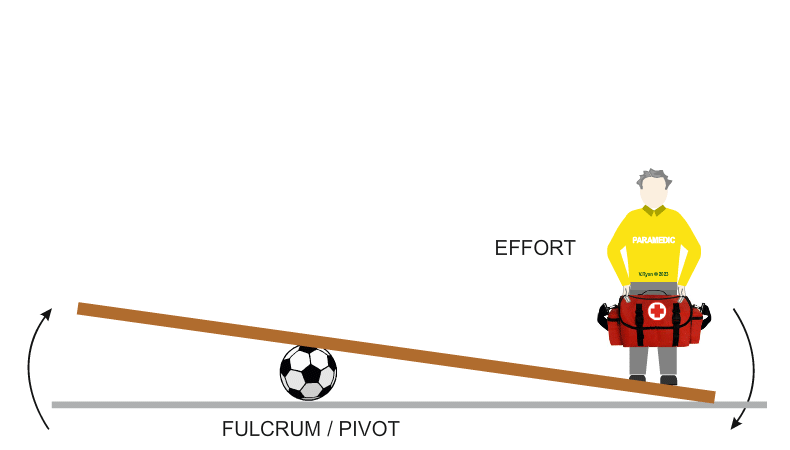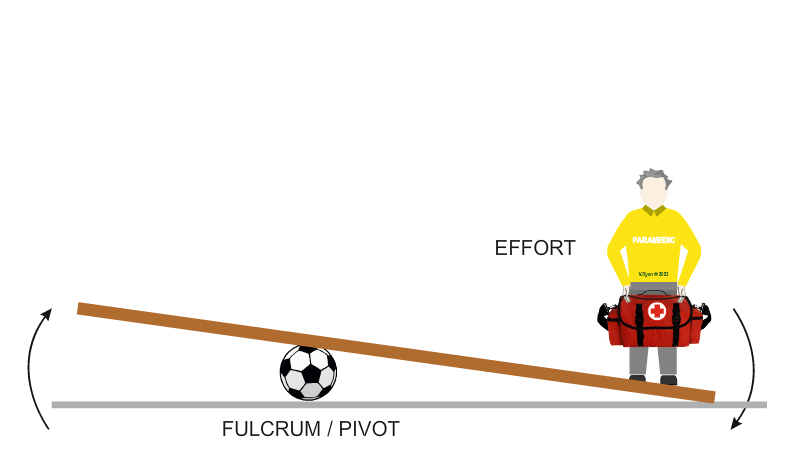
A good example of mechanical advantage is seen below.
An attempt is made to lift the injured patient. A plank has been placed under his body and it will be used as a ‘lever’. A football is used as a fulcrum. A fulcrum is the point at which a lever pivots. |
| |
 |
| |
| Mechanical advantage is the ratio between the load (the patient) and the effort required to lift him from the floor. Increasing the length of the plank(on the effort side) plays an important role, as the longer the plank, the greater the mechanical advantage, the easier it is to lift him (less force is required). |
| |
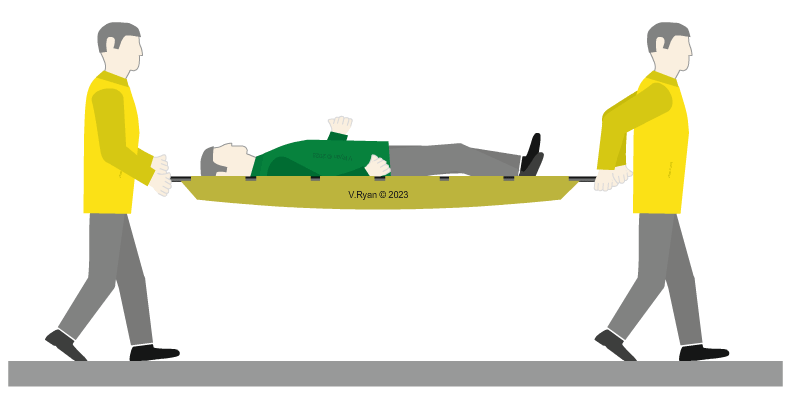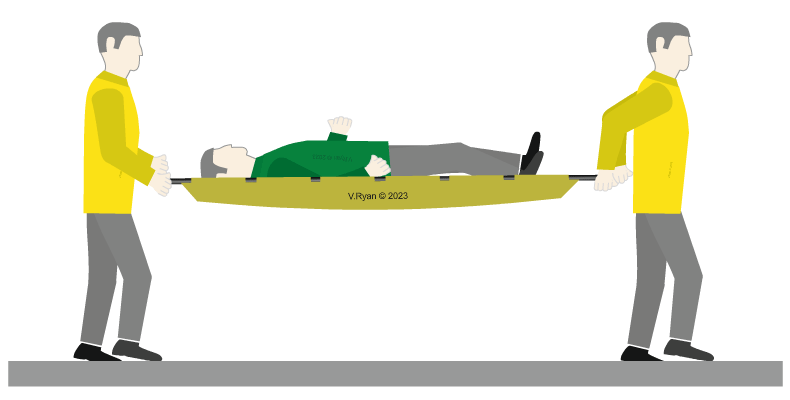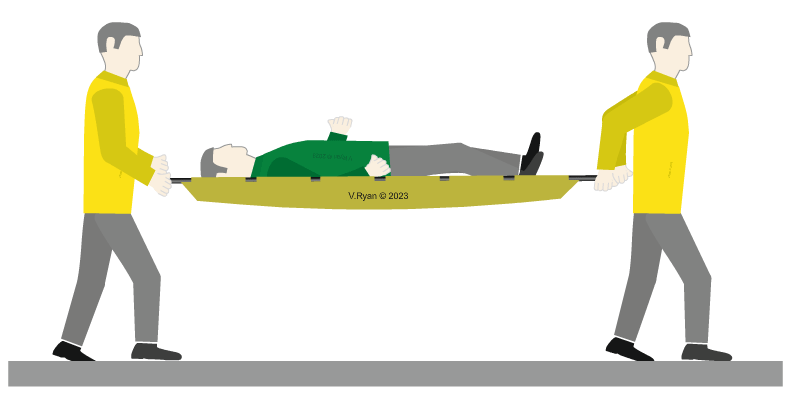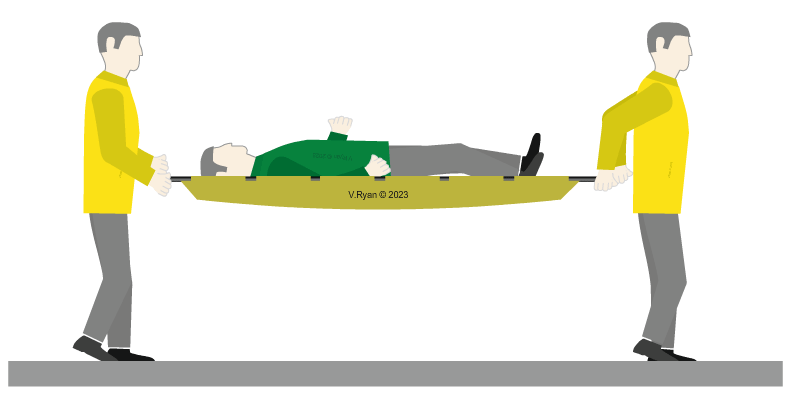
| The patient is carried to the ambulance using a paramedics stretcher. When he is being moved, he is once again a dynamic load. When the stretcher and the paramedics stop walking, he is again, a static load. |
| |
 |
| |
The patient’s ambulance is standing still at a ‘red’ traffic light.
As the ambulance is not moving, it can be regarded as a ‘static load’. Also, it is an example of potential energy.
Once the light changes to green, the ambulance driver will put his foot down on the accelerator and the ambulance moves forward, converting the potential energy to kinetic energy. It is once again, an example of a dynamic load |
| |
 |
|
|
| |
| PRACTICAL EXAMPLE OF MECHANICAL ADVANTAGE |
| |
|
|
The hole punch below has a simple lever, that provides a mechanical advantage, when punching holes in paper and card.
When the lever is pushed down, a cutter near the fulcrum punches holes in the paper / card. Using a lever means that less force is needed to push down. The longer the lever, the less force required. This is an example of mechanical advantage being applied to a design. |
|
 |
| |
|
|
| |
|
|
| |
|
|
| Mechanical advantage is considered to be the ‘ratio’ between the load to be moved and the effort required to move the load. However, the longer the handle, the less effort is required (see moments of force). Both the force and load are measured in units called newtons. |
 |
| |
The example below shows a lever that is in a state of equilibrium (balanced). The load of 600n is balanced by an effort of 200n, because the effort is positioned at a greater distance from the fulcrum.
To work out the mechanical advantage, it is necessary to work out the effort required to ‘balance’ the load first. |
| |
 |
| |
| |
Clockwise moment = 600 x 2 Nm
Anti-clockwise moment = 200 x 6 Nm
In a state of equilibrium,
clockwise moments = anti-clockwise moments
600 X 2 Nm = 200 x 6 Nm
1200 = 1200 |
| |
| Therefore, the Mechanical Advantage is: |
| |
 |
| |
| CLICK HERE FOR FORCES INDEX PAGE |
| |
|
| |
|










